핸즈온 머신러닝[3] 분류(1)

https://www.youtube.com/watch?v=P0g-hpIJ9z0&list=PLJN246lAkhQjX3LOdLVnfdFaCbGouEBeb&index=10 

 

# 파이썬 ≥3.5 필수
import sys
assert sys.version_info >= (3, 5)

# 사이킷런 ≥0.20 필수
import sklearn
assert sklearn.__version__ >= "0.20"

# 공통 모듈 임포트
import numpy as np
import os

# 노트북 실행 결과를 동일하게 유지하기 위해
np.random.seed(42)

# 깔끔한 그래프 출력을 위해
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)

# 그림을 저장할 위치
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "classification"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)

def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
    path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
    print("그림 저장:", fig_id)
    if tight_layout:
        plt.tight_layout()
    plt.savefig(path, format=fig_extension, dpi=resolution)

모듈 임포트, 버전 확인

MNIST

from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', version=1, as_frame=False)
mnist.keys()

X, y = mnist["data"], mnist["target"]
X.shape

(70000, 784): 행이 7만개, 열이 784(28*28)

y.shape

(70000,)

%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt

some_digit = X[0]
some_digit_image = some_digit.reshape(28, 28)
plt.imshow(some_digit_image, cmap=mpl.cm.binary)
plt.axis("off")

save_fig("some_digit_plot")
plt.show()

X의 첫번째 행에 있는 784개의 열을 some_digit에 대입

reshape 함수로 이차원 배열로 만듬

cmap 파라미터에 mpl.cm.binary로 숫자가 높은 픽셀을 더 까맣게 그리도록 함

y[0]

'5'

y = y.astype(np.uint8)

문자열로 되어있는 값들을 정수로 변환함

'5' -> 5

y[0]

5

def plot_digit(data):
    image = data.reshape(28, 28)
    plt.imshow(image, cmap = mpl.cm.binary,
               interpolation="nearest")
    plt.axis("off")

 

 

# 숫자 그림을 위한 추가 함수
def plot_digits(instances, images_per_row=10, **options):
    size = 28
    images_per_row = min(len(instances), images_per_row)
    # n_rows = ceil(len(instances) / images_per_row) 와 동일합니다:
    n_rows = (len(instances) - 1) // images_per_row + 1

    # 필요하면 그리드 끝을 채우기 위해 빈 이미지를 추가합니다:
    n_empty = n_rows * images_per_row - len(instances)
    padded_instances = np.concatenate([instances, np.zeros((n_empty, size * size))], axis=0)

    # 배열의 크기를 바꾸어 28×28 이미지를 담은 그리드로 구성합니다:
    image_grid = padded_instances.reshape((n_rows, images_per_row, size, size))

    # 축 0(이미지 그리드의 수직축)과 2(이미지의 수직축)를 합치고 축 1과 3(두 수평축)을 합칩니다. 
    # 먼저 transpose()를 사용해 결합하려는 축을 옆으로 이동한 다음 합칩니다:
    big_image = image_grid.transpose(0, 2, 1, 3).reshape(n_rows * size,
                                                         images_per_row * size)
    # 하나의 큰 이미지를 얻었으므로 출력하면 됩니다:
    plt.imshow(big_image, cmap = mpl.cm.binary, **options)
    plt.axis("off")​

plt.figure(figsize=(9,9))
example_images = X[:100]
plot_digits(example_images, images_per_row=10)
save_fig("more_digits_plot")
plt.show()

X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]

test 셋과 train 셋이 이미 분류되어있음

 

이진 분류기 훈련

이진 분류기: 두 개의 값중 한가지로 분류함

y_train_5 = (y_train == 5)
y_test_5 = (y_test == 5)

5와 5가 아닌 것으로 분류

from sklearn.linear_model import SGDClassifier

sgd_clf = SGDClassifier(max_iter=1000, tol=1e-3, random_state=42)
sgd_clf.fit(X_train, y_train_5)

max_iter: 최대 반복값

sgd_clf.predict([some_digit])

array([ True])

from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")

array([0.95035, 0.96035, 0.9604 ])

 

 

3-fold

성능 측정

교차 검증을 사용한 정확도 측정

from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone

# shuffle=False가 기본값이기 때문에 random_state를 삭제하던지 shuffle=True로 지정하라는 경고가 발생합니다.
# 0.24버전부터는 에러가 발생할 예정이므로 향후 버전을 위해 shuffle=True을 지정합니다.
skfolds = StratifiedKFold(n_splits=3, random_state=42, shuffle=True)

for train_index, test_index in skfolds.split(X_train, y_train_5):
    clone_clf = clone(sgd_clf)
    X_train_folds = X_train[train_index]
    y_train_folds = y_train_5[train_index]
    X_test_fold = X_train[test_index]
    y_test_fold = y_train_5[test_index]

    clone_clf.fit(X_train_folds, y_train_folds)
    y_pred = clone_clf.predict(X_test_fold)
    n_correct = sum(y_pred == y_test_fold)
    print(n_correct / len(y_pred))

0.9669 0.91625 0.96785

from sklearn.base import BaseEstimator
class Never5Classifier(BaseEstimator):
    def fit(self, X, y=None):
        pass
    def predict(self, X):
        return np.zeros((len(X), 1), dtype=bool)

양성인 클래스가 10%밖에 되지않기 때문에 아까 나온 정확도가 그다지 높은 것이 아님을 알려줌

분균등한 분류 문제에서 나타나는 현상임

never_5_clf = Never5Classifier()
cross_val_score(never_5_clf, X_train, y_train_5, cv=3, scoring="accuracy")

array([0.91125, 0.90855, 0.90915])

 

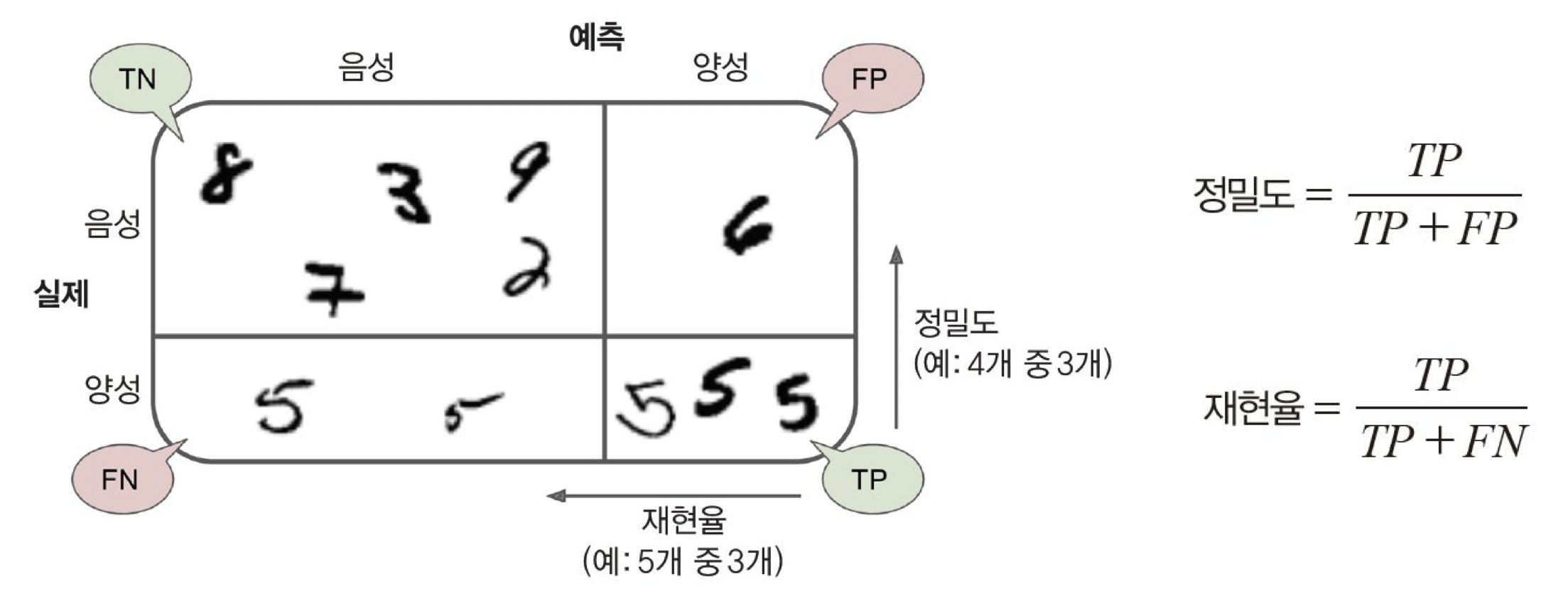
오차 행렬

 

from sklearn.model_selection import cross_val_predict

y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)

from sklearn.metrics import confusion_matrix

confusion_matrix(y_train_5, y_train_pred)

array([[53892, 687], // 실제 음성 클래스를 음성으로 판별, 음성 클래스를 양성으로 판별

           [ 1891, 3530]]) // 양성 클래스를 음성으로 판별, 양성 클래스를 음성으로 판별

y_train_perfect_predictions = y_train_5  # 완벽한척 하자
confusion_matrix(y_train_5, y_train_perfect_predictions)

array([[54579, 0],

           [ 0, 5421]])

완벽하게 맞춘 것으로 pretend

from sklearn.metrics import precision_score, recall_score

precision_score(y_train_5, y_train_pred)

cm = confusion_matrix(y_train_5, y_train_pred)
cm[1, 1] / (cm[0, 1] + cm[1, 1])

0.8370879772350012

recall_score(y_train_5, y_train_pred)

0.6511713705958311

cm[1, 1] / (cm[1, 0] + cm[1, 1])

0.6511713705958311

from sklearn.metrics import f1_score

f1_score(y_train_5, y_train_pred)

0.7325171197343846

정밀도 + 재현율

cm[1, 1] / (cm[1, 1] + (cm[1, 0] + cm[0, 1]) / 2)

0.7325171197343847

정밀도/재현율 트레이드오프

 

y_scores = sgd_clf.decision_function([some_digit])
y_scores

array([2164.22030239])

threshold = 0
y_some_digit_pred = (y_scores > threshold)

y_some_digit_pred

array([ True])

threshold = 8000
y_some_digit_pred = (y_scores > threshold)
y_some_digit_pred

threshold값을 높임

array([False])

y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3,
                             method="decision_function")

from sklearn.metrics import precision_recall_curve

precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)

def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
    plt.plot(thresholds, precisions[:-1], "b--", label="Precision", linewidth=2)
    plt.plot(thresholds, recalls[:-1], "g-", label="Recall", linewidth=2)
    plt.legend(loc="center right", fontsize=16) # Not shown in the book
    plt.xlabel("Threshold", fontsize=16)        # Not shown
    plt.grid(True)                              # Not shown
    plt.axis([-50000, 50000, 0, 1])             # Not shown



recall_90_precision = recalls[np.argmax(precisions >= 0.90)]
threshold_90_precision = thresholds[np.argmax(precisions >= 0.90)]


plt.figure(figsize=(8, 4))                                                                  # Not shown
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.plot([threshold_90_precision, threshold_90_precision], [0., 0.9], "r:")                 # Not shown
plt.plot([-50000, threshold_90_precision], [0.9, 0.9], "r:")                                # Not shown
plt.plot([-50000, threshold_90_precision], [recall_90_precision, recall_90_precision], "r:")# Not shown
plt.plot([threshold_90_precision], [0.9], "ro")                                             # Not shown
plt.plot([threshold_90_precision], [recall_90_precision], "ro")                             # Not shown
save_fig("precision_recall_vs_threshold_plot")                                              # Not shown
plt.show()

(y_train_pred == (y_scores > 0)).all()

True

def plot_precision_vs_recall(precisions, recalls):
    plt.plot(recalls, precisions, "b-", linewidth=2)
    plt.xlabel("Recall", fontsize=16)
    plt.ylabel("Precision", fontsize=16)
    plt.axis([0, 1, 0, 1])
    plt.grid(True)

plt.figure(figsize=(8, 6))
plot_precision_vs_recall(precisions, recalls)
plt.plot([recall_90_precision, recall_90_precision], [0., 0.9], "r:")
plt.plot([0.0, recall_90_precision], [0.9, 0.9], "r:")
plt.plot([recall_90_precision], [0.9], "ro")
save_fig("precision_vs_recall_plot")
plt.show()


#from sklearn.metrics import average_precision_score
#average_precision_score(y_train_5,y_scores)

그래프 아래의 면적을 계산

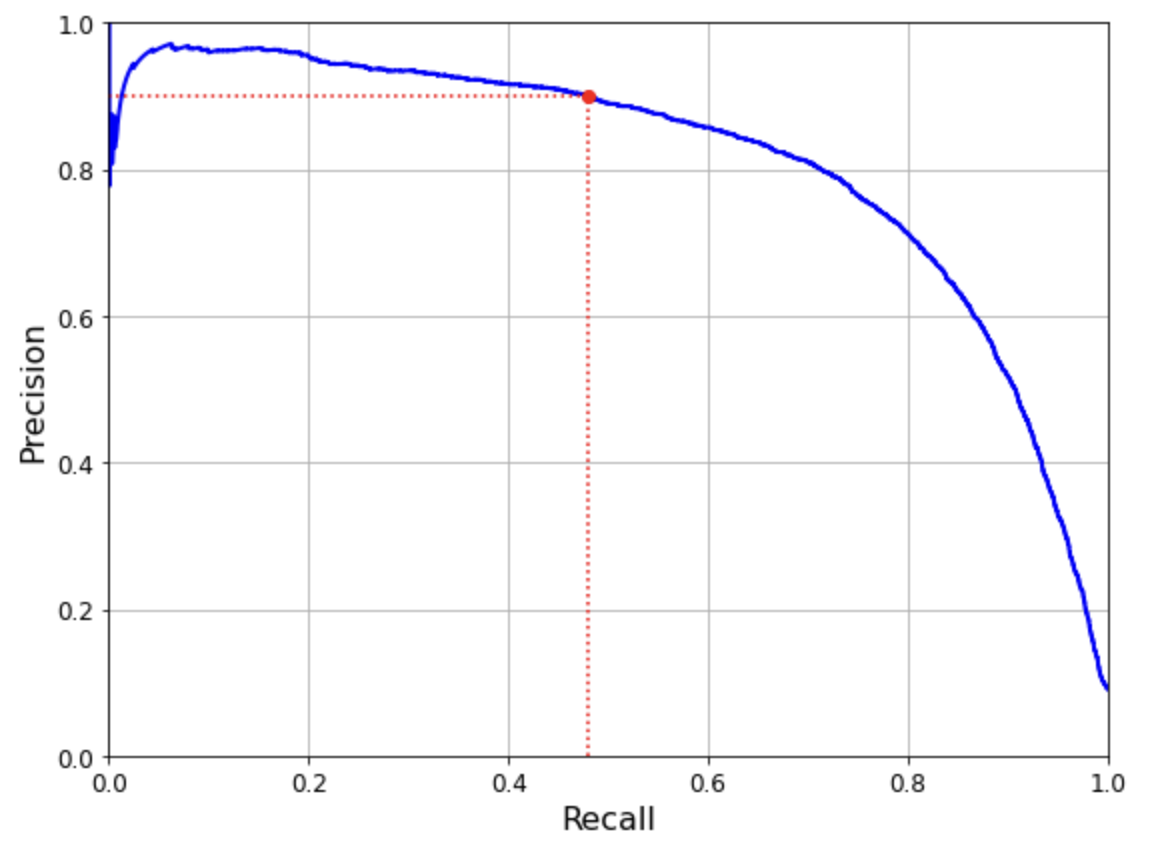
반비례하는 경향

threshold_90_precision = thresholds[np.argmax(precisions >= 0.90)]

threshold_90_precision

3370.0194991439557

y_train_pred_90 = (y_scores >= threshold_90_precision)

precision_score(y_train_5, y_train_pred_90)

0.9000345901072293

recall_score(y_train_5, y_train_pred_90)

0.4799852425751706

 

 

문제

1. 다음과 같은 오차 행렬이 있을 때 정밀도와 재현율을 계산하시오

2. 1의 값을 바탕으로 f1 점수를 계산하시오

3. 정밀도와 재현율이 각각 나타내는 값이 무엇인지 설명하시오

3. 분류모델에서 교차 검증을 사용한 정확도 측정이 신빙성이 없을 수 있는 이유를 설명하시오

4. MNIST가 무엇의 약자이며 무엇을 뜻하는지 설명하시오

 

-오차행렬

1500	300
300	2000