핸즈온 머신러닝[5] 서포트 벡터 머신(2)

 

https://www.youtube.com/watch?v=gjxQo4KwFxQ&list=PLJN246lAkhQjX3LOdLVnfdFaCbGouEBeb&index=17 

 

비선형 분류

X1D = np.linspace(-4, 4, 9).reshape(-1, 1)
X2D = np.c_[X1D, X1D**2]
y = np.array([0, 0, 1, 1, 1, 1, 1, 0, 0])

plt.figure(figsize=(10, 3))

plt.subplot(121)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.plot(X1D[:, 0][y==0], np.zeros(4), "bs")
plt.plot(X1D[:, 0][y==1], np.zeros(5), "g^")
plt.gca().get_yaxis().set_ticks([])
plt.xlabel(r"$x_1$", fontsize=20)
plt.axis([-4.5, 4.5, -0.2, 0.2])

plt.subplot(122)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.plot(X2D[:, 0][y==0], X2D[:, 1][y==0], "bs")
plt.plot(X2D[:, 0][y==1], X2D[:, 1][y==1], "g^")
plt.xlabel(r"$x_1$", fontsize=20)
plt.ylabel(r"$x_2$  ", fontsize=20, rotation=0)
plt.gca().get_yaxis().set_ticks([0, 4, 8, 12, 16])
plt.plot([-4.5, 4.5], [6.5, 6.5], "r--", linewidth=3)
plt.axis([-4.5, 4.5, -1, 17])

plt.subplots_adjust(right=1)

save_fig("higher_dimensions_plot", tight_layout=False)
plt.show()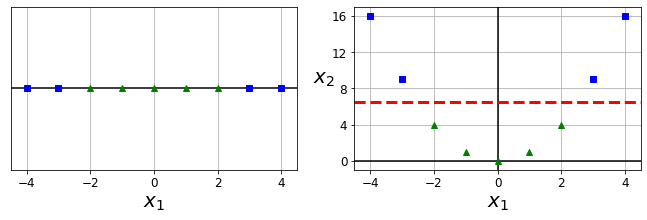

초록색, 파란색으로 음성 클래스, 양성 클래스를 나타낸 그림.

왼쪽에 있는 그림 같은 경우에는 선형적으로 분류할 수 있는 결정 경계를 찾기가 어렵다.

따라서 오른쪽에 있는 그림은 x1을 제곱한 값을 두번째 특성 즉, x1^2=x2로 두어서 선형적으로 분류가 가능할 수 있게끔 만들었다.

 

from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.15, random_state=42)

def plot_dataset(X, y, axes):
    plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
    plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
    plt.axis(axes)
    plt.grid(True, which='both')
    plt.xlabel(r"$x_1$", fontsize=20)
    plt.ylabel(r"$x_2$", fontsize=20, rotation=0)

plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show()

사이킷런의 make_moons 함수는 두 개의 반달 모양의 데이터를 만들어준다. 이렇게 만들어진 데이터는 선형의 결정 경계로는 구분하기 힘들기 때문에 다항 특성을 만들어서 데이터를 분류한다.

 

PolyniomialFeatures 변환기와 StandardScaler, LinearSVC를 연결하여 Pipeline을 만들어 moons 데이터셋에 적용한다.

 

# LinearSVC(liblinear):선형, SVC(libsvm):커널함수(비선형)
# LinearSVC는 좌표경사법 + 뉴튼 메서드를 혼합해서 사용
# C(파라미터)를 늘리면 복잡한 모델, 훈련 시간이 늘어남
# logisticRegression(solver='liblinear') liblinear를 사용한 로지스틱 회귀 문제를 좌표경사하강법으로 빠르게 해결

from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures

polynomial_svm_clf = Pipeline([
        ("poly_features", PolynomialFeatures(degree=3)), # 3차항까지 다항 특성을 만듬
        ("scaler", StandardScaler()),
        ("svm_clf", LinearSVC(C=10, loss="hinge", random_state=42))
    ])

polynomial_svm_clf.fit(X, y)

def plot_predictions(clf, axes):
    x0s = np.linspace(axes[0], axes[1], 100)
    x1s = np.linspace(axes[2], axes[3], 100)
    x0, x1 = np.meshgrid(x0s, x1s)
    X = np.c_[x0.ravel(), x1.ravel()]
    y_pred = clf.predict(X).reshape(x0.shape)
    y_decision = clf.decision_function(X).reshape(x0.shape)
    plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2)
    plt.contourf(x0, x1, y_decision, cmap=plt.cm.brg, alpha=0.1)

plot_predictions(polynomial_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])

save_fig("moons_polynomial_svc_plot")
plt.show()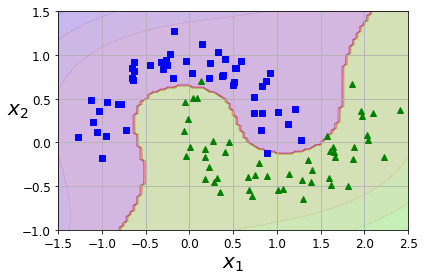

넘파이 linspace 함수는 인자 3개(구간 시작점, 구간 끝점, 구간 내 숫자 개수)를 받아서 균일한 간격으로 숫자를 채워준다.

특성이 많고 데이터셋이 많은 경우에는 linearSVC를 쓰는 것이 효율적

 

 

다항식 커널

다항식 특성을 추가하는 것은 간단하고 잘 작동하지만 낮은 차수의 다항식은 매우 복잡한 데이터셋을 잘 표현하지 못하고 높은 차수의 다항식은 굉장히 많은 특성을 추가하므로 모델을 느리게 만든다.

커널 트릭은 실제로는 특성을 추가하지 않으면서 다항식 특성을 많이 추가한 것과 같은 결과를 얻을 수 있으므로 다항식 특성을 추가하는 것을 대체할 수 있다.

# 커널 트릭: 실제로 다항 특성을 생성하지 않으면서 이와 비슷한 효과를 낼 수 있음
# kernal = poly(다항 커널)
# (gamma * <x,x'> + coef0)^degree
# gamma = 'scale' (기본값): 1/(특성개수*데이터분산)

from sklearn.svm import SVC

poly_kernel_svm_clf = Pipeline([
        ("scaler", StandardScaler()),
        ("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
    ])
poly_kernel_svm_clf.fit(X, y)

poly100_kernel_svm_clf = Pipeline([
        ("scaler", StandardScaler()),
        ("svm_clf", SVC(kernel="poly", degree=10, coef0=100, C=5))
    ])
poly100_kernel_svm_clf.fit(X, y)

degree 값이 각각 3, 10인 두개의 svm 모델을 생성

fig, axes = plt.subplots(ncols=2, figsize=(10.5, 4), sharey=True)

plt.sca(axes[0])
plot_predictions(poly_kernel_svm_clf, [-1.5, 2.45, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.4, -1, 1.5])
plt.title(r"$d=3, r=1, C=5$", fontsize=18)

plt.sca(axes[1])
plot_predictions(poly100_kernel_svm_clf, [-1.5, 2.45, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.4, -1, 1.5])
plt.title(r"$d=10, r=100, C=5$", fontsize=18)
plt.ylabel("")

save_fig("moons_kernelized_polynomial_svc_plot")
plt.show()

 

유사도 특성

비선형 특성을 다루는 또 다른 기법은 각 샘플이 특정 랜드마크와 얼마나 닮았는지 측정하는 유사도 함수로 계산한 특성을 추가하는 것이다. 가우시안 RBF(radial basis function) 함수는 이러한 유사도 함수로 사용할 수 있다.

def gaussian_rbf(x, landmark, gamma):
    return np.exp(-gamma * np.linalg.norm(x - landmark, axis=1)**2)

gamma = 0.3

x1s = np.linspace(-4.5, 4.5, 200).reshape(-1, 1)
x2s = gaussian_rbf(x1s, -2, gamma)
x3s = gaussian_rbf(x1s, 1, gamma)

XK = np.c_[gaussian_rbf(X1D, -2, gamma), gaussian_rbf(X1D, 1, gamma)]
yk = np.array([0, 0, 1, 1, 1, 1, 1, 0, 0])

plt.figure(figsize=(10.5, 4))

plt.subplot(121)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.scatter(x=[-2, 1], y=[0, 0], s=150, alpha=0.5, c="red")
plt.plot(X1D[:, 0][yk==0], np.zeros(4), "bs")
plt.plot(X1D[:, 0][yk==1], np.zeros(5), "g^")
plt.plot(x1s, x2s, "g--")
plt.plot(x1s, x3s, "b:")
plt.gca().get_yaxis().set_ticks([0, 0.25, 0.5, 0.75, 1])
plt.xlabel(r"$x_1$", fontsize=20)
plt.ylabel(r"Similarity", fontsize=14)
plt.annotate(r'$\mathbf{x}$',
             xy=(X1D[3, 0], 0),
             xytext=(-0.5, 0.20),
             ha="center",
             arrowprops=dict(facecolor='black', shrink=0.1),
             fontsize=18,
            )
plt.text(-2, 0.9, "$x_2$", ha="center", fontsize=20)
plt.text(1, 0.9, "$x_3$", ha="center", fontsize=20)
plt.axis([-4.5, 4.5, -0.1, 1.1])

# 두 번째 그래프
plt.subplot(122)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.plot(XK[:, 0][yk==0], XK[:, 1][yk==0], "bs")
plt.plot(XK[:, 0][yk==1], XK[:, 1][yk==1], "g^")
plt.xlabel(r"$x_2$", fontsize=20)
plt.ylabel(r"$x_3$  ", fontsize=20, rotation=0)
plt.annotate(r'$\phi\left(\mathbf{x}\right)$',
             xy=(XK[3, 0], XK[3, 1]),
             xytext=(0.65, 0.50),
             ha="center",
             arrowprops=dict(facecolor='black', shrink=0.1),
             fontsize=18,
            )
plt.plot([-0.1, 1.1], [0.57, -0.1], "r--", linewidth=3)
plt.axis([-0.1, 1.1, -0.1, 1.1])
    
plt.subplots_adjust(right=1)

save_fig("kernel_method_plot")
plt.show()

왼쪽 그림은 -4부터 4까지의 값을 가지는 200개의 포인트를 뽑아서 -2, 1과의 관계를 그린 그래프

 

가우시안 RBF 커널

가우시안 커널은 x와 l이 멀리떨어져있을 때는 영향을 작게 받고, 가까이 있을 때는 영향을 크게 받는 효과를 낸다.

# 커널 파라미터에 'rbf'로 적어서 적용
rbf_kernel_svm_clf = Pipeline([
        ("scaler", StandardScaler()),
        ("svm_clf", SVC(kernel="rbf", gamma=5, C=0.001))
    ])
rbf_kernel_svm_clf.fit(X, y)

from sklearn.svm import SVC

gamma1, gamma2 = 0.1, 5
C1, C2 = 0.001, 1000
hyperparams = (gamma1, C1), (gamma1, C2), (gamma2, C1), (gamma2, C2)

svm_clfs = []
for gamma, C in hyperparams:
    rbf_kernel_svm_clf = Pipeline([
            ("scaler", StandardScaler()),
            ("svm_clf", SVC(kernel="rbf", gamma=gamma, C=C))
        ])
    rbf_kernel_svm_clf.fit(X, y)
    svm_clfs.append(rbf_kernel_svm_clf)

fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(10.5, 7), sharex=True, sharey=True)

for i, svm_clf in enumerate(svm_clfs):
    plt.sca(axes[i // 2, i % 2])
    plot_predictions(svm_clf, [-1.5, 2.45, -1, 1.5])
    plot_dataset(X, y, [-1.5, 2.45, -1, 1.5])
    gamma, C = hyperparams[i]
    plt.title(r"$\gamma = {}, C = {}$".format(gamma, C), fontsize=16)
    if i in (0, 1):
        plt.xlabel("")
    if i in (1, 3):
        plt.ylabel("")

save_fig("moons_rbf_svc_plot")
plt.show()

위의 그림은 감마 값과 규제 값(C)에 따라서 결정 경계가 어떻게 달라지는지를 보여준다.

감마 값, C 값이 커질 수록 규제가 많이 풀어져서 복잡한 결정경계가 만들어진다.

 

SVM 회귀

# 분류: 최대 마진, 회귀: 마진 안에 포함이 목적
np.random.seed(42)
m = 50
X = 2 * np.random.rand(m, 1)
y = (4 + 3 * X + np.random.randn(m, 1)).ravel()

# LinearSVR, SVR
# epsilon: 도로의 폭
# 회귀 함수의 손실 함수: max(0,|y-y_hat|-epsilon)
from sklearn.svm import LinearSVR

svm_reg = LinearSVR(epsilon=1.5, random_state=42)
svm_reg.fit(X, y)

svm_reg1 = LinearSVR(epsilon=1.5, random_state=42)
svm_reg2 = LinearSVR(epsilon=0.5, random_state=42)
svm_reg1.fit(X, y)
svm_reg2.fit(X, y)

def find_support_vectors(svm_reg, X, y):
    y_pred = svm_reg.predict(X)
    off_margin = (np.abs(y - y_pred) >= svm_reg.epsilon)
    return np.argwhere(off_margin)

svm_reg1.support_ = find_support_vectors(svm_reg1, X, y)
svm_reg2.support_ = find_support_vectors(svm_reg2, X, y)

eps_x1 = 1
eps_y_pred = svm_reg1.predict([[eps_x1]])

입실론 값이 1.5일때와 0.5일때 각각의 두 모델을 생성해서 훈련

마진 밖에 있는 샘플들을 수동으로 찾아서 서포트벡터로 지정

def plot_svm_regression(svm_reg, X, y, axes):
    x1s = np.linspace(axes[0], axes[1], 100).reshape(100, 1)
    y_pred = svm_reg.predict(x1s)
    plt.plot(x1s, y_pred, "k-", linewidth=2, label=r"$\hat{y}$")
    plt.plot(x1s, y_pred + svm_reg.epsilon, "k--")
    plt.plot(x1s, y_pred - svm_reg.epsilon, "k--")
    plt.scatter(X[svm_reg.support_], y[svm_reg.support_], s=180, facecolors='#FFAAAA')
    plt.plot(X, y, "bo")
    plt.xlabel(r"$x_1$", fontsize=18)
    plt.legend(loc="upper left", fontsize=18)
    plt.axis(axes)

fig, axes = plt.subplots(ncols=2, figsize=(9, 4), sharey=True)
plt.sca(axes[0])
plot_svm_regression(svm_reg1, X, y, [0, 2, 3, 11])
plt.title(r"$\epsilon = {}$".format(svm_reg1.epsilon), fontsize=18)
plt.ylabel(r"$y$", fontsize=18, rotation=0)
#plt.plot([eps_x1, eps_x1], [eps_y_pred, eps_y_pred - svm_reg1.epsilon], "k-", linewidth=2)
plt.annotate(
        '', xy=(eps_x1, eps_y_pred), xycoords='data',
        xytext=(eps_x1, eps_y_pred - svm_reg1.epsilon),
        textcoords='data', arrowprops={'arrowstyle': '<->', 'linewidth': 1.5}
    )
plt.text(0.91, 5.6, r"$\epsilon$", fontsize=20)
plt.sca(axes[1])
plot_svm_regression(svm_reg2, X, y, [0, 2, 3, 11])
plt.title(r"$\epsilon = {}$".format(svm_reg2.epsilon), fontsize=18)
save_fig("svm_regression_plot")
plt.show()

 

np.random.seed(42)
m = 100
X = 2 * np.random.rand(m, 1) - 1
y = (0.2 + 0.1 * X + 0.5 * X**2 + np.random.randn(m, 1)/10).ravel()

100개의 비선형 샘플을 만들어줌

from sklearn.svm import SVR

svm_poly_reg = SVR(kernel="poly", degree=2, C=100, epsilon=0.1, gamma="scale")
svm_poly_reg.fit(X, y)

다항 커널을 사용한 SVR을 사용

from sklearn.svm import SVR

svm_poly_reg1 = SVR(kernel="poly", degree=2, C=100, epsilon=0.1, gamma="scale")
svm_poly_reg2 = SVR(kernel="poly", degree=2, C=0.01, epsilon=0.1, gamma="scale")
svm_poly_reg1.fit(X, y)
svm_poly_reg2.fit(X, y)

fig, axes = plt.subplots(ncols=2, figsize=(9, 4), sharey=True)
plt.sca(axes[0])
plot_svm_regression(svm_poly_reg1, X, y, [-1, 1, 0, 1])
plt.title(r"$degree={}, C={}, \epsilon = {}$".format(svm_poly_reg1.degree, svm_poly_reg1.C, svm_poly_reg1.epsilon), fontsize=18)
plt.ylabel(r"$y$", fontsize=18, rotation=0)
plt.sca(axes[1])
plot_svm_regression(svm_poly_reg2, X, y, [-1, 1, 0, 1])
plt.title(r"$degree={}, C={}, \epsilon = {}$".format(svm_poly_reg2.degree, svm_poly_reg2.C, svm_poly_reg2.epsilon), fontsize=18)
save_fig("svm_with_polynomial_kernel_plot")
plt.show()

 

문제

1. 사이킷런의 파이프라인과 SVC 클래스를 통해 스테일을 조정하면서 3차 다항식 커널을 사용하는 모델을 만들고 X,y 데이터를 학습시켜라. 단, 필요한 파라미터는 어떤 값을 주어도 상관없음

poly_kernel_svm_clf = Pipeline([

   ("scaler", StandardScaler()),

   ("svm_clf", SVC(kernel="poly", degree=3,coef0=a,C=b))

])

poly_kernel_svm_clf.fit(X,y)

2. 위와 비슷하지만 유사도 함수로 가우시안 커널을 사용하는 모델을 만드시오.

rbf_kernel_svm_clf = Pipeline([

   ("scaler", StandardScaler()),

   ("svm_clf", SVC(kernel="rbf", gamma=5, C=0.001

])

rbf_kernel_svm_clf.fit(X,y)

3. SVM 분류와 SVM 회귀의 목표를 설명하시오.

SVM 분류는 일정한 마진 오류 안에서 두 클래스 간의 도로 폭이 가능한 한 최대가 되도록 하고, SVM 회귀는 제한된 마진 오류 안에서 도로 안에 가능한 한 많은 샘플이 들어가도록 학습한다.