핸즈온 머신러닝[4] 모델 훈련(2)
https://www.youtube.com/watch?v=0CaLoYMBk6c&list=PLJN246lAkhQjX3LOdLVnfdFaCbGouEBeb&index=14
다항 회귀 (Polynomial regression)
import numpy as np
import numpy.random as rnd
np.random.seed(42)m = 100
X = 6 * np.random.rand(m, 1) - 3
# -3 ~ 3
y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1) # 노이즈 추가2차 함수 형태의 그래프를 생성하고 랜덤한 수를 사용해서 노이즈를 추가해준다.
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([-3, 3, 0, 10])
save_fig("quadratic_data_plot")
plt.show()
from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)
X[0]
# 출력: array([-0.75275929])dgree=2 -> 차수가 가장 높은 특성이 2인 것까지 추가해준다.
include_bias -> 편향을 위한 특성 1이 추가된다. 사이킷런의 LinearRegression의 경우 인터셉트를 알아서 구해주기 때문에 이 값을 굳이 추가해주지 않아도 되기 때문에 False로 두었다.
degree=3, a, b, c 세 개의 피쳐가 있으면
피쳐가 1, a, b, c, a^2, b^2, c^2, ab, bc, ac, a^2b, ab^2, a^2b^2, b^2c, bc^2, b^2c^2 ...
X_poly[0]
# 출력: array([-0.75275929, 0.56664654])lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
lin_reg.intercept_, lin_reg.coef_
# 출력: (array([1.78134581]), array([[0.93366893, 0.56456263]]))원래 값과 비교해보면, y = 0.5 * X**2 + X + 2 유사하다는 것을 알 수 있다.
X_new=np.linspace(-3, 3, 100).reshape(100, 1)
X_new_poly = poly_features.transform(X_new)
y_new = lin_reg.predict(X_new_poly)
plt.plot(X, y, "b.")
plt.plot(X_new, y_new, "r-", linewidth=2, label="Predictions")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.legend(loc="upper left", fontsize=14)
plt.axis([-3, 3, 0, 10])
save_fig("quadratic_predictions_plot")
plt.show()
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
for style, width, degree in (("g-", 1, 300), ("b--", 2, 2), ("r-+", 2, 1)):
polybig_features = PolynomialFeatures(degree=degree, include_bias=False)
std_scaler = StandardScaler()
lin_reg = LinearRegression()
polynomial_regression = Pipeline([
("poly_features", polybig_features),
("std_scaler", std_scaler),
("lin_reg", lin_reg),
])
polynomial_regression.fit(X, y)
y_newbig = polynomial_regression.predict(X_new)
plt.plot(X_new, y_newbig, style, label=str(degree), linewidth=width)
plt.plot(X, y, "b.", linewidth=3)
plt.legend(loc="upper left")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([-3, 3, 0, 10])
save_fig("high_degree_polynomials_plot")
plt.show()
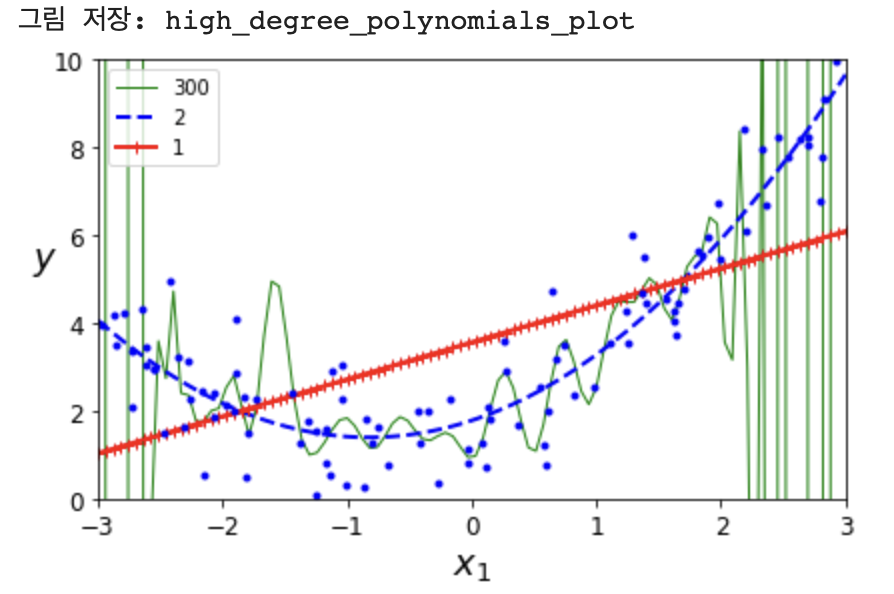
300 --> 과대 적합, 1 --> 과소 적합
300차원의 경우 scaler을 맞춰줘야함 --> std_scaler 또는 LinearRegression의 normalize 파라미터
학습 곡선
Learning curve
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
def plot_learning_curves(model, X, y):
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=10)
train_errors, val_errors = [], []
for m in range(1, len(X_train) + 1):
model.fit(X_train[:m], y_train[:m])
y_train_predict = model.predict(X_train[:m])
y_val_predict = model.predict(X_val)
train_errors.append(mean_squared_error(y_train[:m], y_train_predict))
val_errors.append(mean_squared_error(y_val, y_val_predict))
plt.plot(np.sqrt(train_errors), "r-+", linewidth=2, label="train")
plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="val")
plt.legend(loc="upper right", fontsize=14) # 책에는 없음
plt.xlabel("Training set size", fontsize=14) # 책에는 없음
plt.ylabel("RMSE", fontsize=14) # 책에는 없음lin_reg = LinearRegression()
plot_learning_curves(lin_reg, X, y)
plt.axis([0, 80, 0, 3]) # 책에는 없음
save_fig("underfitting_learning_curves_plot") # 책에는 없음
plt.show()

훈련 세트와 테스트 세트의 사이가 가까우면 과소적합을 의심해볼 수 있음
from sklearn.pipeline import Pipeline
polynomial_regression = Pipeline([
("poly_features", PolynomialFeatures(degree=10, include_bias=False)),
("lin_reg", LinearRegression()),
])
plot_learning_curves(polynomial_regression, X, y)
plt.axis([0, 80, 0, 3]) # 책에는 없음
save_fig("learning_curves_plot") # 책에는 없음
plt.show() # 책에는 없음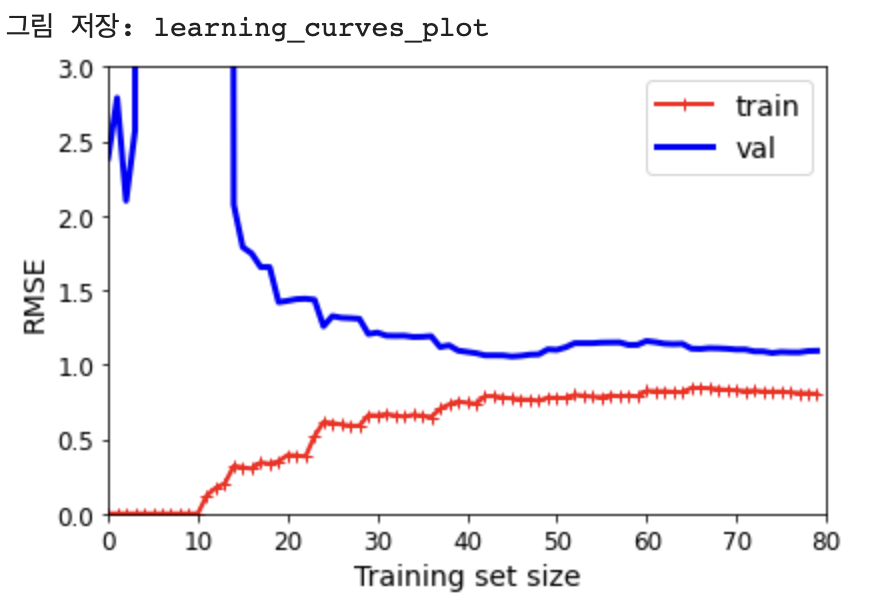
규제가 있는 선형 모델
릿지 회귀
np.random.seed(42)
m = 20
X = 3 * np.random.rand(m, 1)
y = 1 + 0.5 * X + np.random.randn(m, 1) / 1.5
X_new = np.linspace(0, 3, 100).reshape(100, 1)
ɑ 값에 따라 규제를 얼마나 크게할지 조절함
from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=1, solver="cholesky", random_state=42)
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
# 출력: array([[1.55071465]])ridge_reg = Ridge(alpha=1, solver="sag", random_state=42)
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
# 출력: array([[1.5507201]])sag --> Stochastic Average Gradient
from sklearn.linear_model import Ridge
def plot_model(model_class, polynomial, alphas, **model_kargs):
for alpha, style in zip(alphas, ("b-", "g--", "r:")):
model = model_class(alpha, **model_kargs) if alpha > 0 else LinearRegression()
if polynomial:
model = Pipeline([
("poly_features", PolynomialFeatures(degree=10, include_bias=False)),
("std_scaler", StandardScaler()),
("regul_reg", model),
])
model.fit(X, y)
y_new_regul = model.predict(X_new)
lw = 2 if alpha > 0 else 1
plt.plot(X_new, y_new_regul, style, linewidth=lw, label=r"$\alpha = {}$".format(alpha))
plt.plot(X, y, "b.", linewidth=3)
plt.legend(loc="upper left", fontsize=15)
plt.xlabel("$x_1$", fontsize=18)
plt.axis([0, 3, 0, 4])
plt.figure(figsize=(8,4))
plt.subplot(121)
plot_model(Ridge, polynomial=False, alphas=(0, 10, 100), random_state=42)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(122)
plot_model(Ridge, polynomial=True, alphas=(0, 10**-5, 1), random_state=42)
save_fig("ridge_regression_plot")
plt.show()
알파 값이 커짐에 따라 모델의 복잡도가 달라고 경사가 낮아진 것을 볼 수 있음
sgd_reg = SGDRegressor(penalty="l2", max_iter=1000, tol=1e-3, random_state=42)
sgd_reg.fit(X, y.ravel())
sgd_reg.predict([[1.5]])
# 출력: array([1.47012588])
라쏘 회귀

from sklearn.linear_model import Lasso
plt.figure(figsize=(8,4))
plt.subplot(121)
plot_model(Lasso, polynomial=False, alphas=(0, 0.1, 1), random_state=42)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(122)
plot_model(Lasso, polynomial=True, alphas=(0, 10**-7, 1), random_state=42)
save_fig("lasso_regression_plot")
plt.show()
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[1.5]])
# 출력: array([1.53788174])
엘라스틱넷

라소와 릿지를 합한 형태
from sklearn.linear_model import ElasticNet
# Lasso == ElasticNet(l1_ratio=0)
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5, random_state=42)
elastic_net.fit(X, y)
elastic_net.predict([[1.5]])
# 출력: array([1.54333232])
조기 종료
검증 에러가 최솟값에 도달하면 바로 훈련을 중지시키는 것
np.random.seed(42)
m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 2 + X + 0.5 * X**2 + np.random.randn(m, 1)
X_train, X_val, y_train, y_val = train_test_split(X[:50], y[:50].ravel(), test_size=0.5, random_state=10)from copy import deepcopy
poly_scaler = Pipeline([
("poly_features", PolynomialFeatures(degree=90, include_bias=False)),
("std_scaler", StandardScaler())
])
X_train_poly_scaled = poly_scaler.fit_transform(X_train)
X_val_poly_scaled = poly_scaler.transform(X_val)
sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True,
penalty=None, learning_rate="constant", eta0=0.0005, random_state=42)
minimum_val_error = float("inf")
best_epoch = None
best_model = None
for epoch in range(1000):
sgd_reg.fit(X_train_poly_scaled, y_train) # 중지된 곳에서 다시 시작합니다
y_val_predict = sgd_reg.predict(X_val_poly_scaled)
val_error = mean_squared_error(y_val, y_val_predict)
if val_error < minimum_val_error:
minimum_val_error = val_error
best_epoch = epoch
best_model = deepcopy(sgd_reg)
sgd_reg = SGDRegressor(max_iter=1, tol=-np.infty, warm_start=True,
penalty=None, learning_rate="constant", eta0=0.0005, random_state=42)
n_epochs = 500
train_errors, val_errors = [], []
for epoch in range(n_epochs):
sgd_reg.fit(X_train_poly_scaled, y_train)
y_train_predict = sgd_reg.predict(X_train_poly_scaled)
y_val_predict = sgd_reg.predict(X_val_poly_scaled)
train_errors.append(mean_squared_error(y_train, y_train_predict))
val_errors.append(mean_squared_error(y_val, y_val_predict))
best_epoch = np.argmin(val_errors)
best_val_rmse = np.sqrt(val_errors[best_epoch])
plt.annotate('Best model',
xy=(best_epoch, best_val_rmse),
xytext=(best_epoch, best_val_rmse + 1),
ha="center",
arrowprops=dict(facecolor='black', shrink=0.05),
fontsize=16,
)
best_val_rmse -= 0.03 # just to make the graph look better
plt.plot([0, n_epochs], [best_val_rmse, best_val_rmse], "k:", linewidth=2)
plt.plot(np.sqrt(val_errors), "b-", linewidth=3, label="Validation set")
plt.plot(np.sqrt(train_errors), "r--", linewidth=2, label="Training set")
plt.legend(loc="upper right", fontsize=14)
plt.xlabel("Epoch", fontsize=14)
plt.ylabel("RMSE", fontsize=14)
save_fig("early_stopping_plot")
plt.show()
best_epoch, best_model
# 출력: (239,
# SGDRegressor(eta0=0.0005, learning_rate='constant', max_iter=1, penalty=None,
# random_state=42, tol=-inf, warm_start=True))
Lasso vs. ridge

문제
특성이 2개인 데이터를 PolynimialFeatures를 사용해서 degree=4로 설정하면 총 특성의 수는 몇 개가 되는가?
Bias, variance, bias variance trade-off가 각각 무엇인지 설명하시오
라쏘 모델의 중요한 특징은 ______점이며, 라쏘 회귀는 자동적으로 특성 선택을 하고 ( )을 만든다.
파이썬에서 사이킷런의 엘라스틱넷을 사용한다고 할 때, 라소 모델과 똑같은 결과를 내도록하는 파라미터 값은?