[기하학] 선분 교차 2(17387) (C++)

 

https://www.acmicpc.net/problem/17387

17387번: 선분 교차 2

 

 

1. 문제 개요

 

2차원 좌표 평면 위의 두 선분의 양 끝점이 주어졌을 때, 두 선분이 교차하는지 아닌지 구하는 문제.

선분 교차 1 문제와 같지만 세 점 이상의 점이 나란히 있는 경우를 고려해야하는 문제.

 

 

2. 입출력

 

 

3. 문제 풀이

 

선분 교차 1 문제와 같이 점 3개의 방향성을 나타내는 CCW 알고리즘을 사용하여 풀이 할 수 있다.

CCW 알고리즘은 세 점으로 아루어진 삼각형의 면적을 구하는 방법을 이용해서 방향성을 구하는 알고리즘이다.

세 개의 점이 시계 방향, 반시계 방향 또는 평행하게 놓여있는지 여부를 알 수 있다.

 

typedef struct {
    long long x, y;
}pii;
 
long long ccw(pii a, pii b, pii c)
{
    long long ans = (b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x);
    
    if (ans < 0) return 1;
    else if (ans > 0) return -1;
    else return 0;
}

 

ans > 0: 반시계 방향

ans = 0: 일직선

ans < 0: 시계 방향

 

여기에 더해서 세 개 이상의 점이 나란히 있는 경우를 고려해야한다. 이 경우는 ccw 값이 0이 되는 경우인데, ccw만 가지고는 해결할 수 없기 때문에 case를 나누어서 문제를 풀면된다.

 

 

 

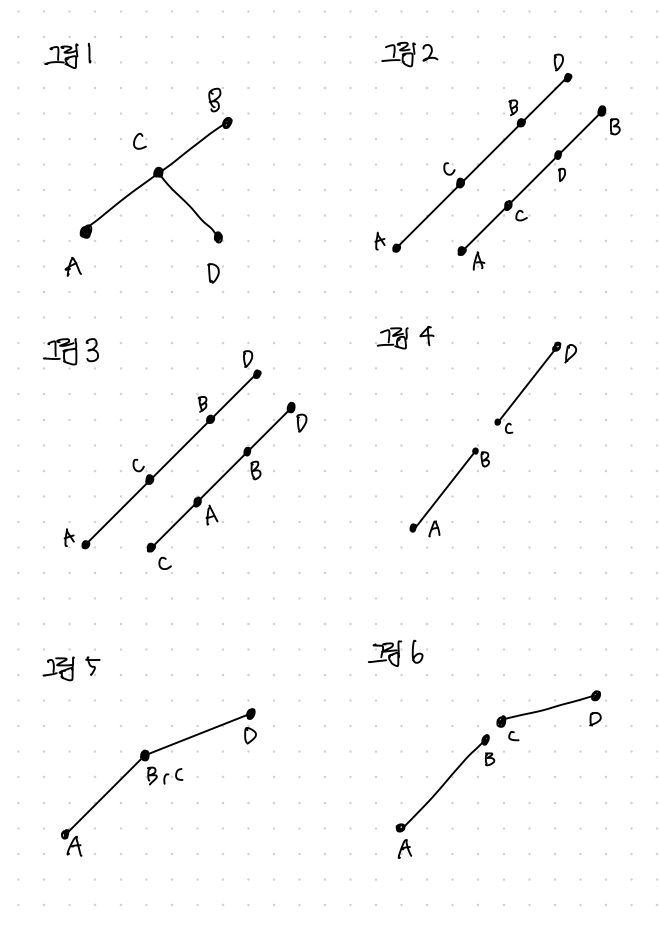
위 그림들의 공통점은 ABC, ABD, CDA, CDB 네 가지 ccw 중 한 개 이상이 0이라는 것이다.

그림 2, 그림 3, 그림 4의 경우에는 점들간의 거리를 계산해서 교차를 판별하였고,

그림 5와 그림 6의 경우에는 (A,C),(A,D),(B,C),(B,D) 중에 같은 위치에 있는 쌍이 있는지 고려하여 판별하였다.

 

 

if((ABC*ABD<0)&&(CDA*CDB<0)) // 세 점이 한 선분 위에 있지 않으며 교차하는 경우
        printf("1\n");
    else if(ABC*ABD*CDA*CDB==0) // 세 점 또는 네 점이 한 선분 위에 있는 경우
    {
        if((ABC*ABD<0)||(CDA*CDB<0)) // 그림 1
            printf("1\n");
        else if((ABC==0&&ABD==0)||(CDA==0&&CDB==0))
        {
            if(max(Dis(A,C),Dis(B,C))<=Dis(A,B)||max(Dis(A,D),Dis(B,D))<=Dis(A,B)) // 그림 2
                printf("1\n");
            else if(max(Dis(C,A),Dis(D,A)) <= Dis(C,D)||max(Dis(C,B),Dis(D,B)) <= Dis(C,D)) // 그림 3
                printf("1\n");
            else
                printf("0\n"); // 그림 4
        }
        else if(Dis(B, C)*Dis(B, D)*Dis(A, C)*Dis(A, D)==0) // 그림 5
            printf("1\n");
        else
            printf("0\n"); // 그림 6
    }
    else
        printf("0\n");

                                                    

 

4. 전체 코드

 

#include <stdio.h>
#include <cmath>

using namespace std;
//선분 교차2

typedef struct {
    long long x, y;
}pii;

long long Dis(pii a, pii b)
{
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
 
long long ccw(pii a, pii b, pii c)
{
    long long ans = (b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x);
    
    if (ans < 0) return 1;
    else if (ans > 0) return -1;
    else return 0;
}

int main(void)
{
    pii A, B, C, D;
    
    scanf("%lld%lld%lld%lld",&A.x,&A.y,&B.x,&B.y);
    scanf("%lld%lld%lld%lld",&C.x,&C.y,&D.x,&D.y);
    
    long long ABC = ccw(A, B, C);
    long long ABD = ccw(A, B, D);
    long long CDA = ccw(C, D, A);
    long long CDB = ccw(C, D, B);
    
    
    if((ABC*ABD<0)&&(CDA*CDB<0)) // 세 점이 한 선분 위에 있지 않으며 교차하는 경우
        printf("1\n");
    else if(ABC*ABD*CDA*CDB==0) // 세 점 또는 네 점이 한 선분 위에 있는 경우
    {
        if((ABC*ABD<0)||(CDA*CDB<0)) // 그림 1
            printf("1\n");
        else if((ABC==0&&ABD==0)||(CDA==0&&CDB==0))
        {
            if(max(Dis(A,C),Dis(B,C))<=Dis(A,B)||max(Dis(A,D),Dis(B,D))<=Dis(A,B)) // 그림 2
                printf("1\n");
            else if(max(Dis(C,A),Dis(D,A)) <= Dis(C,D)||max(Dis(C,B),Dis(D,B)) <= Dis(C,D)) // 그림 3
                printf("1\n");
            else
                printf("0\n"); // 그림 4
        }
        else if(Dis(B, C)*Dis(B, D)*Dis(A, C)*Dis(A, D)==0) // 그림 5
            printf("1\n");
        else
            printf("0\n"); // 그림 6
    }
    else
        printf("0\n");
}

 

 

아직 배워가는 중이라 틀린 부분이 있을 수 있습니다. 지적할 부분이 있다면 댓글로 알려주시면 감사하겠습니다!!!