-
[기하학] 두 원(7869) (C++)BOJ C++ 알고리즘 공부 2022. 2. 11. 19:19
https://www.acmicpc.net/problem/7869
7869번: 두 원
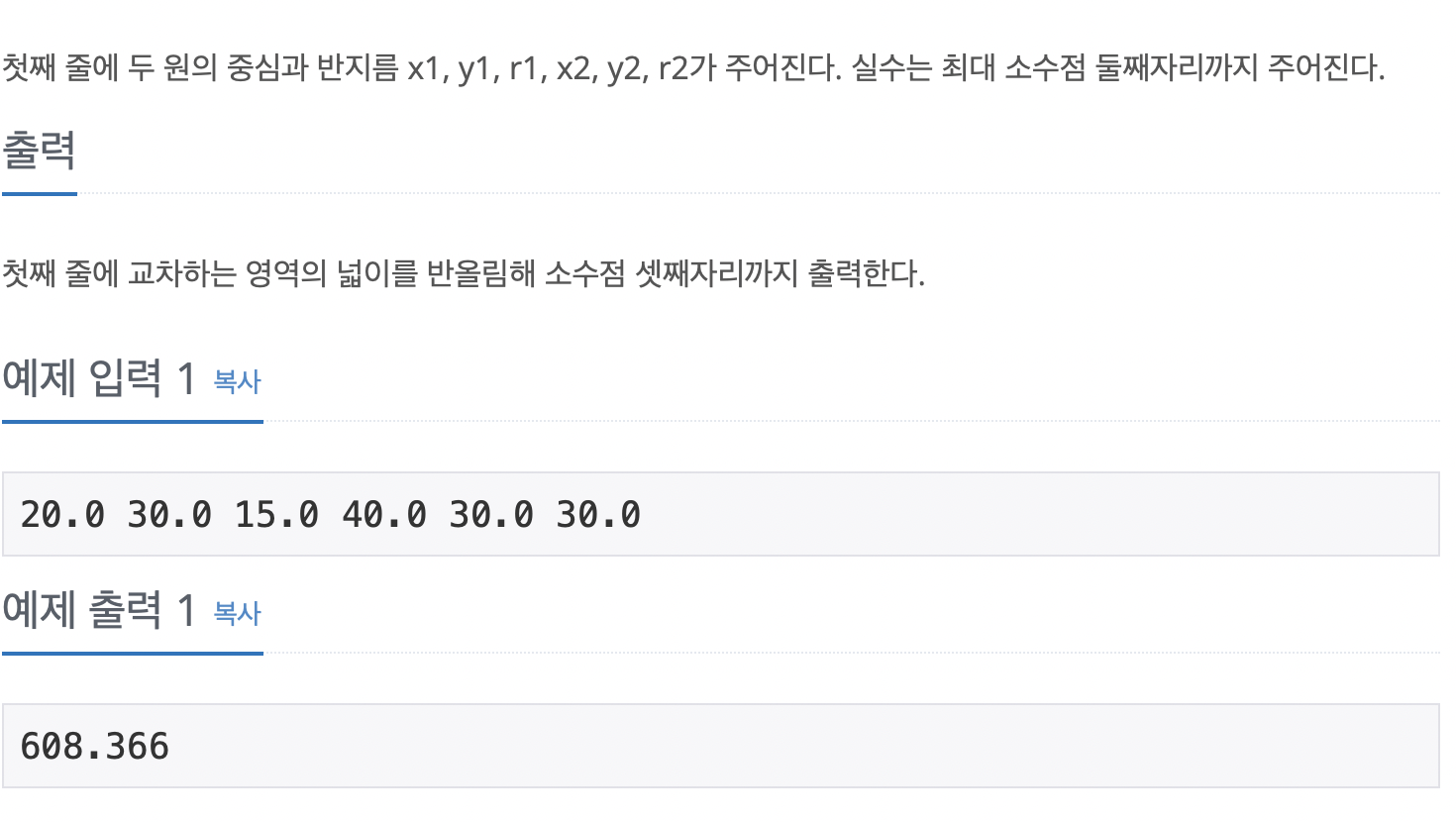
첫째 줄에 두 원의 중심과 반지름 x1, y1, r1, x2, y2, r2가 주어진다. 실수는 최대 소수점 둘째자리까지 주어진다.
www.acmicpc.net
1. 문제 개요
2차원 평면상에 두 원이 주어질 때, 교차하는 영역의 넓이를 소수점 셋째자리 구하는 문제.

2. 입출력
3. 문제 풀이
두 원이 만나는 경우는 네가지로 나눌 수 있다.

첫번째는 두 원이 만나지 않는 경우이다.
이 경우에는 두 원의 중심의 거리가 두 원의 반지름을 합한 값보다 크다. 두 원이 교차하는 영역이 존재하지 않게 된다.
두번째는 한 원이 다른 원에 포함되지 않으면서 한 점에서 만나는 경우이다.
이 경우에는 두 원의 중심의 거리가 두 원의 반지름을 합한 값과 같다. 두 원이 교차하는 영역이 존재하지 않게 된다.
세번째로는 한 원이 다른 원에 포함되는 경우이다.
이 경우에는 두 원의 중심의 거리가 두 원의 반지름을 뺀값의 절댓값보다 작다. 다른 원에 포함된 원의 넓이가 두 원이 교차하는 영역의 넓이가 된다.
마지막으로는 두 원이 두 점에서 만나는 경우이다.
이 경우에는 아래와 같이 넓이를 구할 수 있다.
1. 두 원이 만나는 부분의 넓이는 두 원의 활꼴을 더해주면 구할 수 있다.

2. 활꼴의 넓이는 부채꼴에서 해당 각도의 삼각형을 빼주면 구할 수 있다.
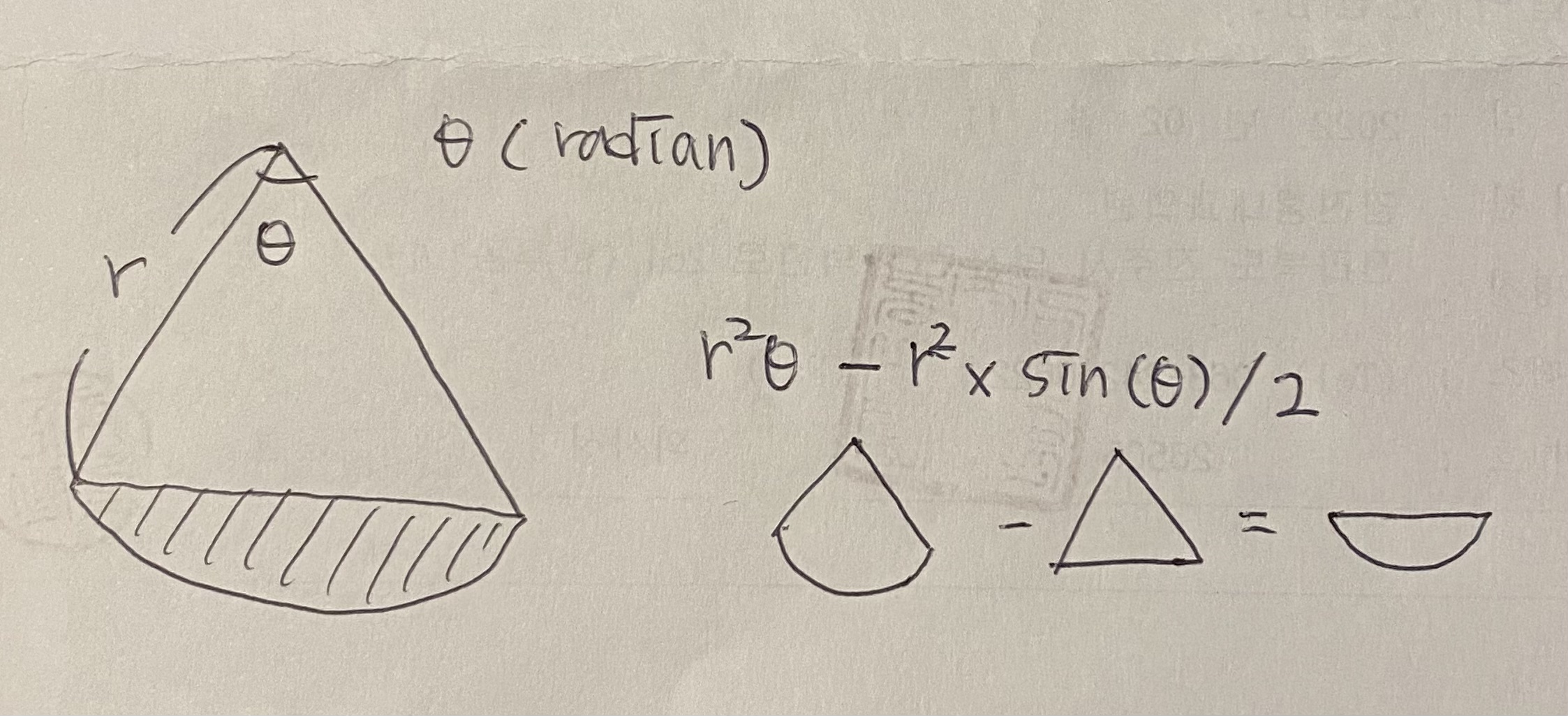
여기서 중요한 것은 각 원의 부채꼴의 각도를 어떻게 구할 것인가이다.
3. 부채꼴의 각도는 코사인법칙을 통해 구할 수 있다.
코사인법칙의 정의:

반지름이 r1인 원의 부채꼴의 각도를 포함한 코사인법칙은 다음과 같고, 아코사인함수에 코사인 값을 구하면 세타값을 구할 수 있다.
마지막으로 세타에 2를 곱해주기만 하면된다.
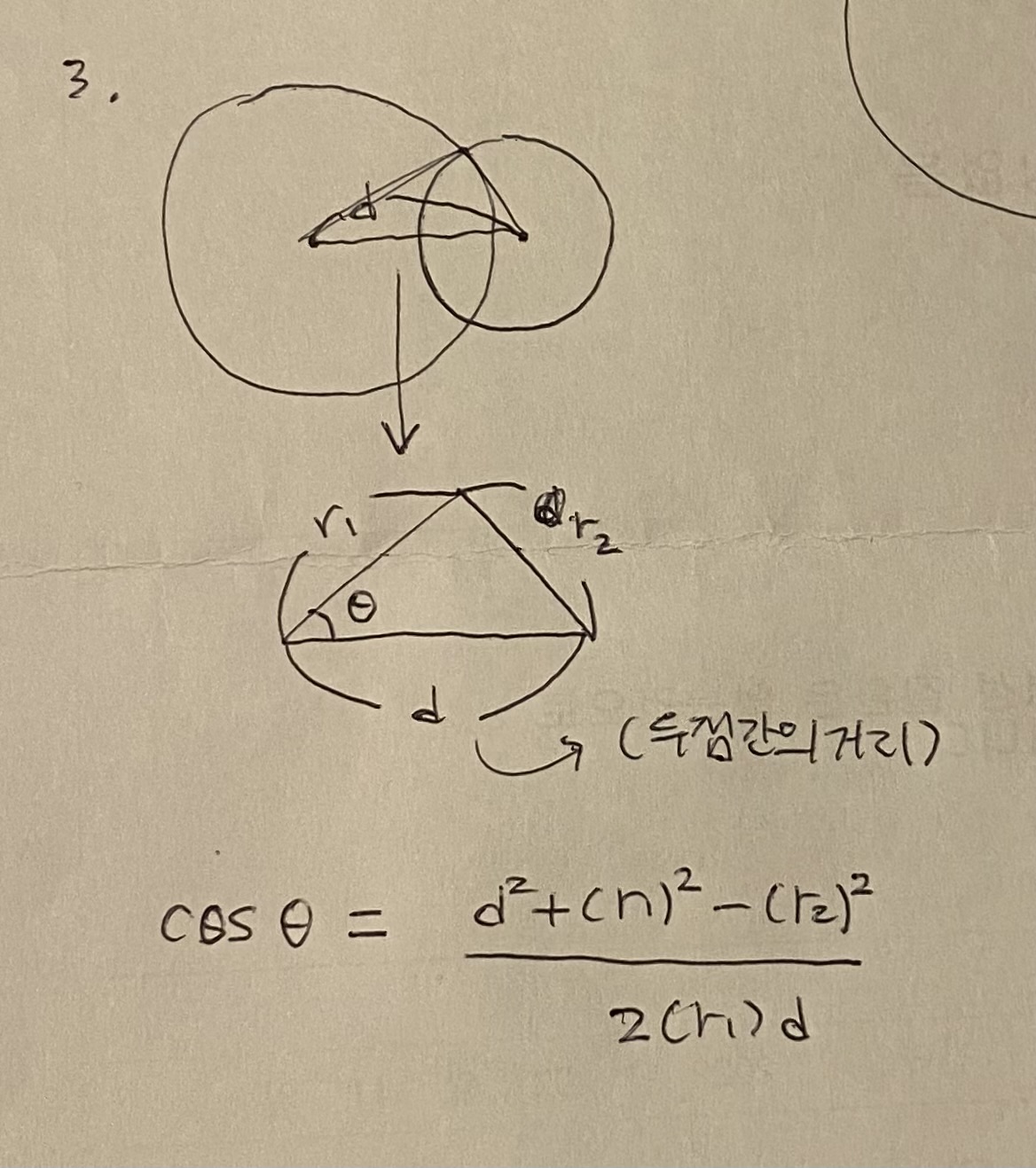
반지름이 r2인 원의 부채꼴의 각도 또한 r1과 r2 위치를 바꾸어주기만 하면 똑같이 구할 수 있다.
4. 전체 코드
#include <algorithm> #include <stdio.h> #include <vector> #include <cmath> using namespace std; //두 원 int main() { double x1, y1, r1, x2, y2, r2; scanf("%lf%lf%lf%lf%lf%lf",&x1,&y1,&r1,&x2,&y2,&r2); double d = sqrt(pow(x1-x2, 2) + pow(y1-y2, 2)); if(d>=r1+r2) { printf("0.000"); } else if (d <= abs(r1-r2)) { //한 원이 다른 원을 포함하는 경우 double radius = min(r1,r2); printf("%.3lf",round((radius*radius*M_PI)*1000)/1000); } else { double theta1 = acos((r1*r1 + d * d - r2 * r2)/(2*r1*d)); double theta2 = acos((r2*r2 + d*d - r1*r1)/(2*r2*d)); double triangular1 = r1 * r1 * sin(2*theta1)/2; double triangular2 = r2 * r2 * sin(2*theta2)/2; double s1 = (r1 * r1 * theta1) - triangular1; double s2 = (r2 * r2 * theta2) - triangular2; printf("%.3lf",round((s1+s2)*1000)/1000); } return 0; }'BOJ C++ 알고리즘 공부' 카테고리의 다른 글
[기하학] 선분 교차1 (17386) (C++) (0) 2022.02.15 [기하학] CCW(11758) (C/C++) (0) 2022.02.12 [기하학] 다각형의 넓이(2166) C++ (0) 2022.02.10 [플로이드-와샬] 운동(1956) (0) 2022.02.07 [자료구조] 이진 검색 트리(5639) (0) 2022.02.03